



Next: 6.3.5 Cassini Cylindrical Projection
Up: 6.3 Cylindrical Projections
Previous: 6.3.3 Universal Transverse Mercator
Contents
Index
Oblique configurations of the cylinder give rise to the
oblique Mercator projection. It is particularly useful when
mapping regions of large lateral extent in an oblique direction.
Both parallels and meridians are complex curves. The projection
was developed in the early 1900s by several workers. Several
parameters must be provided to define the projection. GMT offers three different definitions:
- Option -Joa or -JOa:
- Longitude and latitude of projection center
- Azimuth of the oblique equator
- Scale in inch/degree or 1:xxxxx along
oblique equator (-Joa), or map width (-JOa)
- Option -Job or -JOb:
- Longitude and latitude of projection center
- Longitude and latitude of second point on oblique equator
- Scale in inch/degree or 1:xxxxx along oblique
equator (-Job), or map width (-JOb)
- Option -Joc or -JOc:
- Longitude and latitude of projection center
- Longitude and latitude of projection pole
- scale in inch/degree or 1:xxxxx along oblique
equator (-Joc), or map width (-JOc)
Our example was produced by the command
pscoast -R270/20/305/25r -JOc280/25.5/22/69/4.8i -B10g5 -Dl -A250 -Glightgray -W0.25p -P \
-Tf301.5/23/0.4i/2 --HEADER_FONT_SIZE=8p --LABEL_OFFSET=0.05i > GMT_obl_merc.ps
Figure 6.16:
Oblique Mercator map using -Joc. We
make it clear which direction is North by adding a star rose with the -T option.
|
|
It uses definition 3 for an oblique view of some Caribbean islands.
Note that we define our region using the rectangular system
described earlier. If we do not append an ``r'' to the -R
string then the information provided with the -R option is
assumed to be oblique degrees about the projection center rather
than the usual geographic coordinates. This interpretation is
chosen since in general the parallels and meridians are not very
suitable as map boundaries.




Next: 6.3.5 Cassini Cylindrical Projection
Up: 6.3 Cylindrical Projections
Previous: 6.3.3 Universal Transverse Mercator
Contents
Index
Paul Wessel
2006-01-01
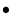
![\includegraphics[]{eps/GMT_obl_merc}](img143.png)