



Next: K.4 The Five Resolutions
Up: K. The GMT High-Resolution
Previous: K.2 Format required by
Contents
Index
The WVS and WDB together represent more than 100 Mb of binary
data and something like 20 million data points. Hence, it
becomes obvious that any manipulation of these data must be
automated. For instance, the reasonable requirement that no
coastline should cross another coastline becomes a complicated
processing step.
- To begin, we first made sure that all data were ``clean'',
i.e. that there were no outliers and bad points. We had to
write several programs to ensure data consistency and remove
``spikes'' and bad points from the raw data. Also, crossing
segments were automatically ``trimmed'' provided only
a few points had to be deleted. A few hundred more complicated
cases had to be examined semi-manually.
- Programs were written to examine all the loose segments
and determine which segments should be joined to produce
polygons. Because not all segments joined exactly (there were
non-zero gaps between some segments) we had to find all possible
combinations and choose the simplest combinations.
The WVS segments joined to produce more than 200,000 polygons,
the largest being the Africa-Eurasia polygon which has 1.4
million points. The WDB data resulted in a smaller data base
(
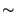 25% of WVS).
25% of WVS).
- We now needed to combine the WVS and WDB data bases.
The main problem here is that we have duplicates of polygons:
most of the features in WVS are also in WDB. However, because
the resolution of the data differ it is nontrivial to figure
out which polygons in WDB to include and which ones to ignore.
We used two techniques to address this problem.
First, we looked for crossovers between all possible pairs of
polygons. Because of the crossover processing in step 1 above we know
that there are no remaining crossovers within WVS and WDB; thus
any crossovers would be between WVS and WDB polygons. Crossovers
could mean two things: (1) A slightly misplaced WDB polygon
crosses a more accurate WVS polygon, both representing the same
geographic feature, or (2) a misplaced WDB polygon (e.g. a small
coastal lake) crosses the accurate WVS shoreline. We distinguished
between these cases by comparing the area and centroid of the two
polygons. In almost all cases it was obvious when we had
duplicates; a few cases had to be checked manually. Second,
on many occasions the WDB duplicate polygon did not cross its
WVS counterpart but was either entirely inside or outside the
WVS polygon. In those cases we relied on the area-centroid tests.
- While the largest polygons were easy to identify by visual
inspection, the majority remain unidentified. Since it is
important to know whether a polygon is a continent or a small
pond inside an island inside a lake we wrote programs that would
determine the hierarchical level of each polygon. Here, level = 1
represents ocean/land boundaries, 2 is land/lakes borders, 3 is
lakes/islands-in-lakes, and 4 is islands-in-lakes/ponds-in-islands-in-lakes.
Level 4 was the highest level encountered in the data.
To automatically determine the hierarchical levels we wrote
programs that would compare all possible pairs of polygons
and find how many polygons a given polygon was inside. Because
of the size and number of the polygons such programs would
typically run for 3 days on a Sparc-2 workstation.
- Once we know what type a polygon is we can enforce a
common ``orientation'' for all polygons. We arranged them so
that when you move along a polygon from beginning to end, your
left hand is pointing toward ``land''. At this step we also
computed the area of all polygons since we would like the
option to plot only features that are bigger than a minimum
area to be specified by the user.
- Obviously, if you need to make a map of Denmark then
you do not want to read the entire 1.4 million points making
up the Africa-Eurasia polygon. Furthermore, most plotting
devices will not let you paint and fill a polygon of that size
due to memory restrictions. Hence, we need to partition the
polygons so that smaller subsets can be accessed rapidly.
Likewise, if you want to plot a world map on a letter-size paper
there is no need to plot 10 million data points as most of them
will plot several times on the same pixel and the operation
would take a very long time to complete. We chose to make 5
versions on the database, corresponding to different resolutions.
The decimation was carried out using the Douglas-Peucker (DP)
line-reduction algorithmK.2. We chose the
cutoffs so that each subset was approximately 20% the size of
the next higher resolution. The five resolutions are called
full, high, intermediate, low, and
crude; they are accessed in pscoast, gmtselect,
and grdlandmask with the -D optionK.3. For each of
these 5 data sets (f, h, i, l, c)
we specified an equidistant grid (1
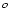 , 2
, 2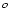 , 5
, 5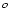 ,
10
,
10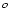 , 20
, 20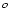 ) and split all polygons into line-segments
that each fit inside one of the many boxes defined by these grid
lines. Thus, to paint the entire continent of Australia we
instead paint many smaller polygons made up of these line
segments and gridlines. Some book-keeping has to be done since
we need to know which parent polygon these smaller pieces came
from in order to prescribe the correct paint or ignore if the
feature is smaller than the cutoff specified by the user. The
resulting segment coordinates were then scaled to fit in short
integer format to preserve precision and written in netCDF format
for ultimate portability across hardware platformsK.4.
) and split all polygons into line-segments
that each fit inside one of the many boxes defined by these grid
lines. Thus, to paint the entire continent of Australia we
instead paint many smaller polygons made up of these line
segments and gridlines. Some book-keeping has to be done since
we need to know which parent polygon these smaller pieces came
from in order to prescribe the correct paint or ignore if the
feature is smaller than the cutoff specified by the user. The
resulting segment coordinates were then scaled to fit in short
integer format to preserve precision and written in netCDF format
for ultimate portability across hardware platformsK.4.
- While we are now back to a file of line-segments we are in
a much better position to create smaller polygons for painting.
Two problems must be overcome to correctly paint an area:
- We must be able to join line segments and grid cell borders
into meaningful polygons; how we do this will depend on whether
we want to paint the land or the oceans.
- We want to nest the polygons so that no paint falls on areas
that are ``wet'' (or ``dry''); e.g., if a grid cell completely on
land contains a lake with a small island, we do not want to paint
the lake and then draw the island, but paint the annulus or ``donut''
that is represented by the land and lake, and then plot the island.
GMT uses a polygon-assembly routine that carries out these
tasks on the fly.




Next: K.4 The Five Resolutions
Up: K. The GMT High-Resolution
Previous: K.2 Format required by
Contents
Index
Paul Wessel
2006-01-01